Fractals Revisited Again
Saturday, 24th of October, 2015
Having conquered the Mandlebrot set and the Julia set (at least in my own opinion) I decided to expand upon the image mapping possibilites available to me and attempt to create fractals with higher powers of n where z = zⁿ+c. I thought I would be able to use the same distortion correction measurements which had worked for the basic Mandlebrot set but I was SO wrong.
As you can see from the following 4 images, the distortion just becomes more and more intensified.
Multibrot variation of Mandelbrot set, z = z³+c:
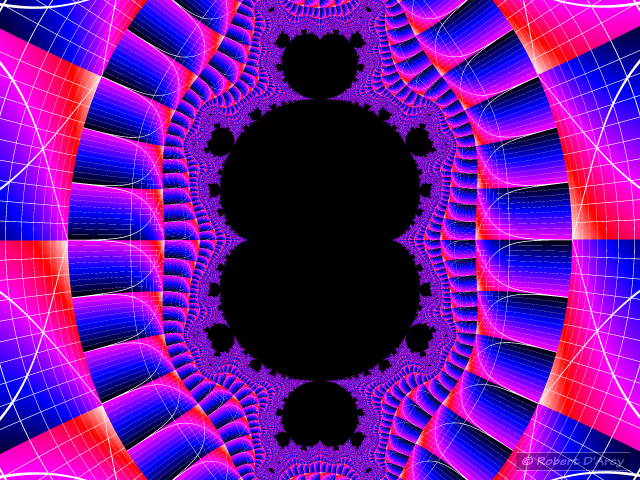
Multibrot variation of Mandelbrot set, z = z⁴+c:

Multibrot variation of Mandelbrot set, z = z⁵+c:

Multibrot variation of Mandelbrot set, z = z⁶+c:

Because of the increasing distortion, new anti-distortion measurements would need to be created for each new exponent of z, which is a very time consuming process. Another problem is that with each successive exponent of z the mapped images become more and more squashed.
I measured the distortion for the z = z³+c Multibrot and with a little bit of jiggery and pokery I managed to stretch the mapped image back to a more-or-less square shape. As you can see the distances between all of the white grid lines in each test card image are evenly spaced, so things are looking good already:

I continued on and measured the distortion for the z = z⁴+c Multibrot. Again the distances between all of the white grid lines in each test card image are evenly spaced but despite using the same anti-squashing as for the z = z³+c Multibrot the mapped images are getting squashed again:

The horizontal part of each mapped image is based upon the decomposition of the final angle of z once it has escaped past the bailout distance. Removing half of the images and showing only the ones where z is on the positive side of the X-axis you can see that the width of each mapped image above is 180 degrees, or 1 radian.
The problem is that the decomposition is based upon where the final z lands, not on where it starts or on any other factor, and all mapped images must begin and end between 0 and 2 radians. In the image below in the second largest band it looks as if there are 32 radians all the way around the image but in fact it is the same 2 radians repeated 16 times:
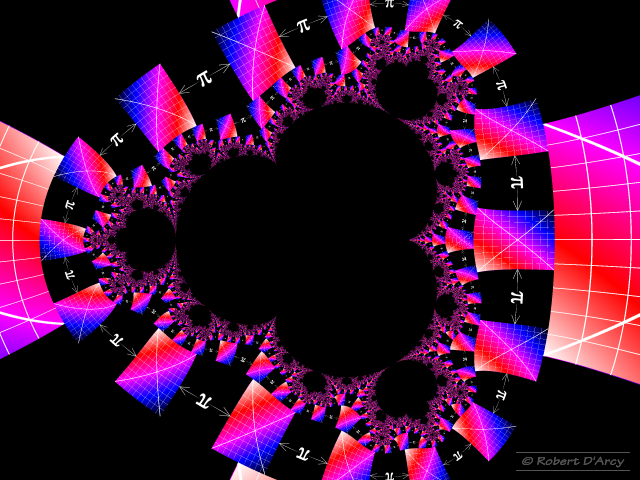
As a temporary fix I can double the anti-squashing so that each mapped image takes up the full 2 radians. To avoid the images looking stretched I can use a wider non-square source image and this is exactly what I have done here:

Unfortunately I can't rely on this solution because with each increase in the exponent of z the source images would need to be narrower and narrower. It looks as if z = z⁵+c might be the furthest I take this mapping system.
It looks like it is time to go back to the drawing board....